When we look at the world that surrounds us, we do not probably think about mathematics, do we? Well, this holds unless you are a scientist or a very keen person on science. Then, I am sure you might definitely see mathematics behind any single phenomenon that happens around you. In fact, anything can be described with formulae. Nevertheless, how can we come up with the equations that rule the world when they are hard to be uncovered?
When we perform experiments for our research and data analyses, we collect useful data about the system we want to further analyse and understand. There are some situations, though, in which things get complicated, such as:
- Big data to be processed.
- Unknown physics behind the natural phenomenon.
- Known equations, but not trivial solution.
- Known equations, but computationally expensive solution.
The above mentioned cases happen more often than we think. To begin with, let’s imagine we want to better understand a phenomenon that occurs in a specific system, or model (i.e., a reproduction of the system in a laboratory or in a computer simulation), we are keen on studying, but we do not know how this system really works. To overcome this problem, we can think about which parameters might be relevant to our measurements: which ones might directly or indirectly affect the output? As a matter of fact, many parameters might usually be affecting the phenomena that occur in our system, but not all of them will be relevant. Besides, the way the different parameters interact one with another might make the understanding of the phenomenon even more difficult. In fact, if we were to alter one of the parameters used for data collection, we might affect both the output (i.e., the effect of these parameters on the phenomena we are to study in the system) and other parameters we have included in the analysis too. Hence, the cross relation between parameters results in extra layers of complexity that prevent us to see the formulae behind the system in a clear and intuitive way. The possibility of describing the output of the system by studying the influence of each parameter separately sounds challenging here, but fascinating indeed. The great news is that this is possible!
How should we proceed then? All we have got is a completely unknown physical phenomenon going on in the system of interest. In addition, we might have a lot of generated data from which no theory can be extracted. How can we then squeeze such a system into a known and simple formula? Our group has implemented an algorithm able to extract a mathematical model from pure data. Even more, the mathematical model obtained is not as complex as the original data and the obtained formula simplifies the physical phenomenon without any relevant information being lost. Let me tell you how we have achieved this.
We have used a mathematical technique called Reduced Order Modelling (ROM), which is a numerical strategy that can transform complex and multi-variable systems into significantly less complex mathematical functions that can describe and predict tangled and unknown systems’ behaviours. Our approach is based on Tensor Rank Decomposition (TRD), a strategy performed on tensors, i.e., mathematical objects that can be simply regarded as multi-linear maps that encode the information about the system’s parametric relationships. Note that our multidimensional tensor will have as many dimensions as parameters are included in the system. Specifically, TRD can decompose our N-dimensional tensor (i.e., N here corresponds to the number of dimensions our tensor will have, thus a number greater than 1) into M one-dimensional tensors (i.e., M is lower than or equal to N), whose relationship is now known. For instance, let’s imagine we were to decompose a 9-dimensional tensor, that is, N = 9 in this example. Our approach would be able to generate nine or less than nine tensors of one dimension, where M would be lower than or equal to 9. In essence, TRD provides us with a methodology to describe the system’s behaviour through a known formula by reducing the complexity of our system and enabling us to study the effect of these parameters separately!
In our algorithm, we provide an approach that applies TRD to any kind of data, e.g., dense, sparse or unstructured data (Fig. 1); by treating them as rank-N tensors, meaning that we use tensors with as many dimensions as parameters we want to include in our system.
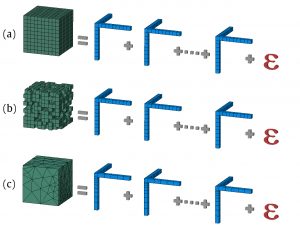
Figure 1. Graphical visualization of dense (a), sparse (b), and unstructured (c) data tensor decomposition.
To summarize, such an algorithm is able to simplify a system’s behaviour, resulting into a known formula. Moreover, the obtained formula leads to a deeper understanding of the studied phenomenon, since separating the contribution of each parameter exposes the physics behind it. In the end, this approach is thought to be used for many different purposes and fields of study, ranging from fluid-dynamics (e.g., blood flow) to material sciences (e.g., material characterization) or even medicine (e.g., predictive medicine).
* * *
By Valentina Zambrano, Postdoc at the Instituto Tecnológico de Aragón (ITAINNOVA).
More information: