Cuando miras a tu alrededor, es muy probable que las matemáticas no sea lo primero que te venga a la cabeza… Bueno, esto no es del todo cierto… Puede que así sea si eres científico o te interesa mucho la ciencia. En este caso, estoy segura de que podrías ver las matemáticas detrás de cada fenómeno que ocurre a tu alrededor. De hecho, cualquier situación se puede describir a través de fórmulas matemáticas. Sin embargo, ¿cómo podemos encontrar estas ecuaciones que rigen el mundo cuando no se dejan ver?
En proyectos de investigación, se llevan a cabo experimentos a partir de los cuales se pueden obtener datos importantes sobre el sistema que queremos analizar y entender. No obstante, siempre podemos encontrarnos con situaciones que nos compliquen el estudio y análisis de datos como, por ejemplo, las que encuentras enumeradas a continuación:
- Procesar Big Data.
- Física desconocida detrás del fenómeno a estudiar.
- Ecuaciones conocidas, pero solución compleja.
- Ecuaciones conocidas, pero solución computacionalmente costosa.
Las situaciones anteriores se dan más frecuentemente de lo que nos gustaría. Por ejemplo, imaginemos que queremos entender mejor un fenómeno que sucede en un sistema, o modelo (i.e., una reproducción del sistema en laboratorio o en simulación computacional), que queremos estudiar; pero en verdad no sabemos cómo funciona este sistema. Para hacer frente a este problema, nos centramos en buscar qué parámetros pueden llegar a ser útiles para nuestros análisis computacionales: ¿cuáles afectan directamente y/o indirectamente el resultado que observamos? Por si esto no fuera suficientemente complejo, muchas veces estos parámetros pueden estar interconectados y contribuir simultáneamente al fenómeno que queremos estudiar en nuestro sistema. Por suerte, no todos estos parámetros tiene por qué ser relevantes para entender el fenómento de estudio. Eso sí, la forma en la que los diferentes parámetros interactúan entre ellos puede dificultar la comprensión y resolución de nuestro problema. De hecho, si modificamos uno de los parámetros que incluimos en nuestro análisis para generar datos, podríamos estar afectando tanto al resultado observado (i.e., también conocido como output o «salida», es decir, el efecto que estos parámetros tienen sobre el fenómeno que estamos estudiando en el sistema) así como también a otros parámetros que hemos decidido incluir en el análisis. Por tanto, el hecho de que los parámetros estén interconectados hace que nos sea mucho más difícil «ver» de una forma clara e intuitiva las fórmulas que necesitamos para poder describir nuestro sistema de interés. Aunque es todo un reto llegar a entender cómo cada parámetro afecta al sistema de estudio, tengo buenas noticias: ¡no es sencillo pero sí que es posible!
Entonces, ¿con qué metodo procedemos? Todo lo que tenemos por el momento es un fenómeno físico completamente desconocido que queremos estudiar en un sistema que nos interesa. Además, puede que tengamos también una gran cantidad de datos que no podamos analizar ni comprender mediante ninguna teoría conocida hasta el momento. Ahora bien, ¿cómo podemos encajar un sistema de este tipo en una simple fórmula matemática? Nuestro grupo ha implementado un algoritmo capaz de extraer un modelo matemático a partir de datos puros. Es más, el modelo matemático obtenido no es tan complejo como los datos originales y la fórmula obtenida simplifica el fenómeno físico sin que se pierda ninguna información relevante. A continuación os cuento cómo lo hemos logrado.
Hemos usado una técnica matemática llamada Modelos de Orden Reducido (MOR); una estrategia numérica que puede transformar sistemas complejos y multivariables en funciones matemáticas significativamente menos complicadas y que pueden llegar a describir y predecir comportamientos de sistemas desconocidos. Nuestro enfoque se basa en la descomposición de tensores, es decir, de objetos matemáticos que pueden ser vistos como mapas multilineales que contienen la información sobre las relaciones paramétricas del sistema de interés. Hay que tener en cuenta que estos tensores multidimensionales tendrán tantas dimensiones como parámetros se hayan incluidos en el sistema. En concreto, hemos usado la técnica Tensor Rank Decomposition (TRD), la cual es una estrategia que permite descomponer nuestro tensor de N dimensiones en M tensores unidimensionales (es importante resaltar que M siempre será igual o menor a N), cuyas relaciones son ahora conocidas. Por ejemplo, si tuviéramos que descomponer un tensor de 9 dimensiones (i.e., N sería igual a 9 en este ejemplo) mediante TRD, acaríamos generando un total de 9 o menos tensores de una única dimensión, simplificando así nuestro sistema. De este modo, el comportamiento del sistema puede ser descrito a través de una fórmula que permite reducir su complejidad y que, a su vez, nos permite estudiar el efecto de cada parámetro por separado.
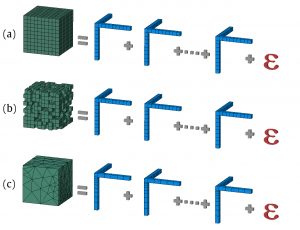
El método implementado en nuestro algoritmo utiliza la descomposición tensorial descrita anteriormente para analizar cualquier tipo de datos, p.ej., datos completos, escasos y no estructurados (Fig. 1); tratándolos como tensores de rango N. Esto quiere decir que usamos tensores que tienen tantas dimensiones como parámetros hemos incluido en nuestro sistema.
En resumen, el algoritmo descrito en esta entrada es capaz de simplificar el comportamiento de un sistema en una simple fórmula matemática. Además, la fórmula obtenida permite comprender mejor el fenómeno de interés al permitirnos separar la contribución de cada parámetro, exponiendo así la física escondida tras el sistema de interés. Nuestro método computacional se ha diseñado con la idea de ser utilizado en varios campos de investigación, abarcando desde dinámica de fluidos (p.ej., flujo sanguíneo) a ciencias de materiales (p.ej., caracterización de materiales) o incluso diferentes campos de la medicina (p.ej., medicina predictiva).
* * *
Por Valentina Zambrano, Postdoc en el Instituto Tecnológico de Aragón (ITAINNOVA).
Más información: